Multivariate Normal Distribution: Introduction

import tensorflow_probability.substrates.jax as tfp
import matplotlib.pyplot as plt
import seaborn as sns
import jax.numpy as jnp
%matplotlib inline

dist = tfp.distributions

prior = dist.MultivariateNormalFullCovariance(loc = jnp.zeros(2), covariance_matrix=jnp.eye(2) + 1.)

WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)

xs = jnp.linspace(-2., 2., num=100)
ys = jnp.linspace(-2.,2., num=100)
xx, yy = jnp.meshgrid(xs, ys, indexing="xy")

Z_prior = jnp.exp(prior.log_prob(jnp.vstack((xx.ravel(), yy.ravel())).transpose()).reshape(xx.shape))

# Code borrowed from https://jakevdp.github.io/PythonDataScienceHandbook/04.04-density-and-contour-plots.html
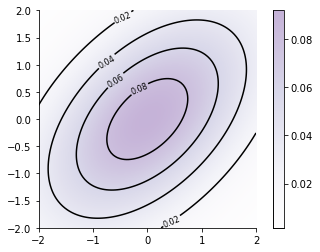
contours = plt.contour(xx, yy, Z_prior, 5, colors='black')
plt.clabel(contours, inline=True, fontsize=8)

plt.imshow(Z_prior, extent=[-2, 2, -2, 2], origin='lower',
           cmap='Purples', alpha=0.3)
plt.colorbar();
sns.despine()

ax = plt.axes(projection='3d')
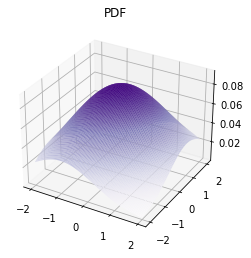
ax.plot_surface(xx, yy, Z_prior, rstride=1, cstride=1,
                cmap='Purples', edgecolor='none')
ax.set_title('PDF');

TODO

1. Add all content from https://nipunbatra.github.io/blog/ml/2019/08/20/Gaussian-Processes.html