Learning Gaussian Process regression parameters using mini-batch stochastic gradient descent#
How to learn the parameters of a GP
toc: true
badges: true
comments: true
author: Nipun Batra
categories: [ML]
Defining log-likelihood#
In our previous post we had mentioned (for the noiseless case):
Given train data $\( D=\left(x_{i}, y_{i}\right), i=1: N \)\( Given a test set \)X_{}\( of size \)N_{} \times d\( containing \)N_{}\( points in \)\mathbb{R}^{d},\( we want to predict function outputs \)y_{}\( We can write: \)\( \left(\begin{array}{l} y \\ y_{*} \end{array}\right) \sim \mathcal{N}\left(\left(\begin{array}{l} \mu \\ \mu_{*} \end{array}\right),\left(\begin{array}{cc} K & K_{*} \\ K_{*}^{T} & K_{* *} \end{array}\right)\right) \)\( where \)\( \begin{aligned} K &=\operatorname{Ker}(X, X) \in \mathbb{R}^{N \times N} \\ K_{*} &=\operatorname{Ker}\left(X, X_{*}\right) \in \mathbb{R}^{N \times N} \\ K_{* *} &=\operatorname{Ker}\left(X_{*}, X_{*}\right) \in \mathbb{R}^{N_{*} \times N_{*}} \end{aligned} \)$
Thus, from the property of conditioning of multivariate Gaussian, we know that:
We will assume \(\mu\) to be zero. Thus, we have for the train data, the following expression:
For the noisy case, we have:
From this expression, we can write the log-likelihood of data computed over the kernel parameters \(\theta\) as:
Thus, we can write:
where $\(M = K + \sigma_{noise}^2\mathcal{I}_N\)$
Imports#
As before, we will be using the excellent Autograd library for automatically computing the gradient of an objective function with respect to the parameters. We will also be using GPy for verifying our calculations.
Let us start with some basic imports.
import autograd.numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
import warnings
warnings.filterwarnings('ignore')
import GPy
Defining our RBF kernel#
The definition of the (1-dimensional) RBF kernel has a Gaussian-form, defined as:
def rbf(x1, x2, sigma, l):
return (sigma**2)*(np.exp(-(x1-x2)**2/(2*(l**2))))
Defining GPy’s RBF kernel#
# Create a 1-D RBF kernel with default parameters
k = GPy.kern.RBF(1)
# Preview the kernel's parameters
k
| rbf. | value | constraints | priors |
|---|---|---|---|
| variance | 1.0 | +ve | |
| lengthscale | 1.0 | +ve |
Matching our RBF kernel with GPy’s kernel#
rbf(1, 0, 1, 1)==k.K(np.array([[1]]), np.array([[0]])).flatten()
array([ True])
Looks good. Our function is matching GPy’s kernel.
GP Regresion#
Creating a data set#
# lambda function, call f(x) to generate data
f = lambda x: 0.4*x**2 - 0.15*x**3 + 0.5*x**2 - 0.002*x**5 + 0.0002*x**6 +0.5*(x-2)**2
n = 50
np.random.seed(0)
X = np.linspace(0.05, 4.95, n)[:,None]
Y = f(X) + np.random.normal(0., 0.1, (n,1)) # note that np.random.normal takes mean and s.d. (not variance), 0.1^2 = 0.01
plt.plot(X, Y, "kx", mew=0.5, label='Train points')
plt.xlabel("x"), plt.ylabel("f")
plt.legend();
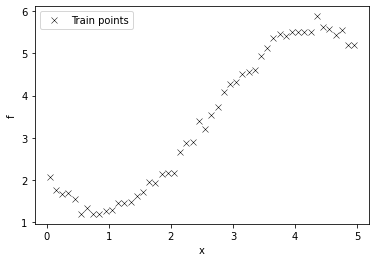
Function to compute negative log likelihood#
Based on our above mentioned theory, we can now write the NLL function as follows
def nll(X, Y, sigma, l, noise_std):
n = X.shape[0]
cov = rbf(X, X.T, sigma, l) + (noise_std**2)*np.eye(X.shape[0])
nll_ar = 0.5*(Y.T@np.linalg.inv(cov)@Y) + 0.5*n*np.log(2*np.pi) + 0.5*np.log(np.linalg.det(cov))
return nll_ar[0,0]
Comparing the NLL from our method with the NLL from GPy#
We will now compare the NLL from our method with GPy for a fixed set of parameters
nll(X,Y, 1, 1, 1)
70.9892893011209
k.lengthscale = 1
k.variance = 1
m = GPy.models.GPRegression(X, Y, k, normalizer=False)
m.Gaussian_noise = 1
print(m)
Name : GP regression
Objective : 70.98928950981251
Number of Parameters : 3
Number of Optimization Parameters : 3
Updates : True
Parameters:
GP_regression. | value | constraints | priors
rbf.variance | 1.0 | +ve |
rbf.lengthscale | 1.0 | +ve |
Gaussian_noise.variance | 1.0 | +ve |
Excellent, we can see that our method gives the same NLL. Looks like we are on the right track! One caveat here is that I have set the normalizer to be False, which means that GPy will not be mean centering the data.
Optimizing the GP using GPy#
We will now use GPy to optimize the GP parameters
m = GPy.models.GPRegression(X, Y, k, normalizer=False)
m.optimize()
print(m)
Name : GP regression
Objective : -20.145595097323056
Number of Parameters : 3
Number of Optimization Parameters : 3
Updates : True
Parameters:
GP_regression. | value | constraints | priors
rbf.variance | 38.67759006151069 | +ve |
rbf.lengthscale | 2.9466566795409825 | +ve |
Gaussian_noise.variance | 0.012471600151185298 | +ve |
It seems that variance close to 28 and length scale close to 2.7 give the optimum objective for the GP
Plotting the NLL as a function of variance and lenghtscale#
We will now plot the NLL obtained from our calculations as a function of variance and lengthscale. For comparing our solution with GPy solution, I will be setting noise variance to be 0.0075
We will now try to find the “optimum” \(\sigma\) and lengthscale from this NLL space.
X.shape
(50, 1)
batch_size = 20
idx = np.random.randint(X.shape[0], size=batch_size)
X_subset, Y_subset = X[idx, :], Y[idx]
X_subset, Y_subset
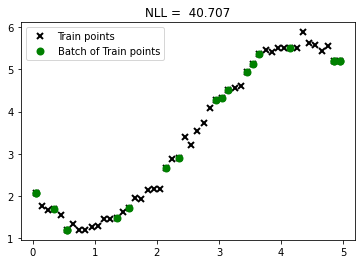
plt.plot(X, Y, "kx", mew=2, label='Train points')
plt.plot(X_subset, Y_subset, "go", mew=2, label='Batch of Train points')
plt.legend()
plt.title("NLL = %0.3f" %nll(X_subset, Y_subset, 1, 1, 1))
Text(0.5, 1.0, 'NLL = 40.707')
Gradient descent using autograd#
from autograd import elementwise_grad as egrad
from autograd import grad
grad_objective = grad(nll, argnum=[2, 3, 4])
Visualising the objective as a function of iteration#
sigma = 2.
l = 2.
noise = 0.5
lr = 1e-2
num_iter = 1500
np.random.seed(0)
nll_arr = np.zeros(num_iter)
for iteration in range(num_iter):
idx = np.random.randint(X.shape[0], size=batch_size)
X_subset, Y_subset = X[idx, :], Y[idx]
nll_arr[iteration] = nll(X_subset, Y_subset, sigma, l, noise)
del_sigma, del_l, del_noise = grad_objective(X_subset, Y_subset, sigma, l, noise)
sigma = sigma - lr*del_sigma
l = l - lr*del_l
noise = noise - lr*del_noise
lr = lr/(iteration+1)
print(sigma**2, l, noise)
4.3561278602353966 1.983897766041748 -0.10206454293334008
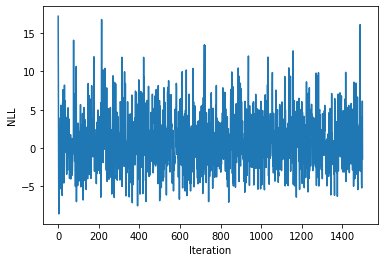
plt.plot(nll_arr)
plt.xlabel("Iteration")
plt.ylabel("NLL")
Text(0, 0.5, 'NLL')
Choosing N-Neighbors for SGD batch#
sigma = 2.
l = 2.
noise = 0.5
lr = 1e-2
num_iter = 1500
np.random.seed(0)
nll_arr = np.zeros(num_iter)
for iteration in range(num_iter):
# Sample 1 point
idx = np.random.randint(X.shape[0], size=1)
x_val = X[idx]
K = batch_size
a = np.abs(X - x_val).flatten()
idx = np.argpartition(a,K)[:K]
X_subset = X[idx, :]
Y_subset = Y[idx, :]
nll_arr[iteration] = nll(X_subset, Y_subset, sigma, l, noise)
del_sigma, del_l, del_noise = grad_objective(X_subset, Y_subset, sigma, l, noise)
sigma = sigma - lr*del_sigma
l = l - lr*del_l
noise = noise - lr*del_noise
lr = lr/(iteration+1)
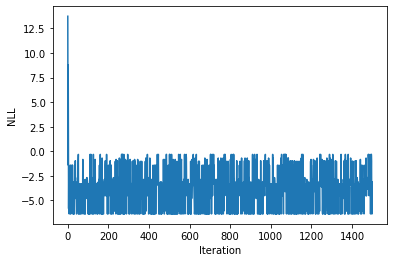
plt.plot(nll_arr)
plt.xlabel("Iteration")
plt.ylabel("NLL")
Text(0, 0.5, 'NLL')
Applying gradient descent and visualising the learnt function#
sigma = 2.
l = 2.
noise = 0.5
lr = 1e-2
num_iter = 100
batch_size = 5
nll_arr = np.zeros(num_iter)
fig, ax = plt.subplots()
np.random.seed(0)
for iteration in range(num_iter):
# Sample 1 point
idx = np.random.randint(X.shape[0], size=1)
x_val = X[idx]
K = batch_size
a = np.abs(X - x_val).flatten()
idx = np.argpartition(a,K)[:K]
X_subset = X[idx, :]
Y_subset = Y[idx, :]
nll_arr[iteration] = nll(X_subset, Y_subset, sigma, l, noise)
del_sigma, del_l, del_noise = grad_objective(X_subset, Y_subset, sigma, l, noise)
sigma = sigma - lr*del_sigma
l = l - lr*del_l
noise = noise - lr*del_noise
k.lengthscale = l
k.variance = sigma**2
m = GPy.models.GPRegression(X, Y, k, normalizer=False)
m.Gaussian_noise = noise**2
m.plot(ax=ax, alpha=0.2)['dataplot'];
ax.scatter(X_subset, Y_subset, color='green', marker='*', s = 50)
plt.ylim((0, 6))
#plt.title(f"Iteration: {iteration:04}, Objective :{nll_arr[iteration]:04.2f}")
plt.savefig(f"/Users/nipun/Desktop/gp_learning/{iteration:04}.png")
ax.clear()
lr = lr/(iteration+1)
plt.clf()
<Figure size 432x288 with 0 Axes>
print(sigma**2, l, noise)
4.239252534833201 2.0031950532157596 0.30136335707188894
!convert -delay 40 -loop 0 /Users/nipun/Desktop/gp_learning/*.png gp-learning-new.gif


