Encoder-Decoder Networks

Encoder-Decoder Networks#

Imports#

import os
os.environ['CUDA_VISIBLE_DEVICES'] = '3'

import numpy as np

import torch
from torch import Tensor
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F
from torch.utils.data import DataLoader, TensorDataset

from beartype import beartype
from jaxtyping import Float, jaxtyped

from sklearn.preprocessing import OneHotEncoder

from tqdm.notebook import tqdm

import matplotlib.pyplot as plt

from typing import Union, Tuple

device = "cuda"

Problem: Next Character Prediction#

Before diving into the specifics, it’d be helpful to define a tiny problem (without loss of generality).

Problm: Given a sequence of characters, predict the next character in the sequence.
Example input: “hell”
Example output: “o”

Recurrent Neural Networks (RNNs)#

Resource: Andrej Karpathy | CS231n Winter 2016: Lecture 10: Recurrent Neural Networks, Image Captioning, LSTM

Image source: https://cs231n.github.io/assets/rnn/types.png

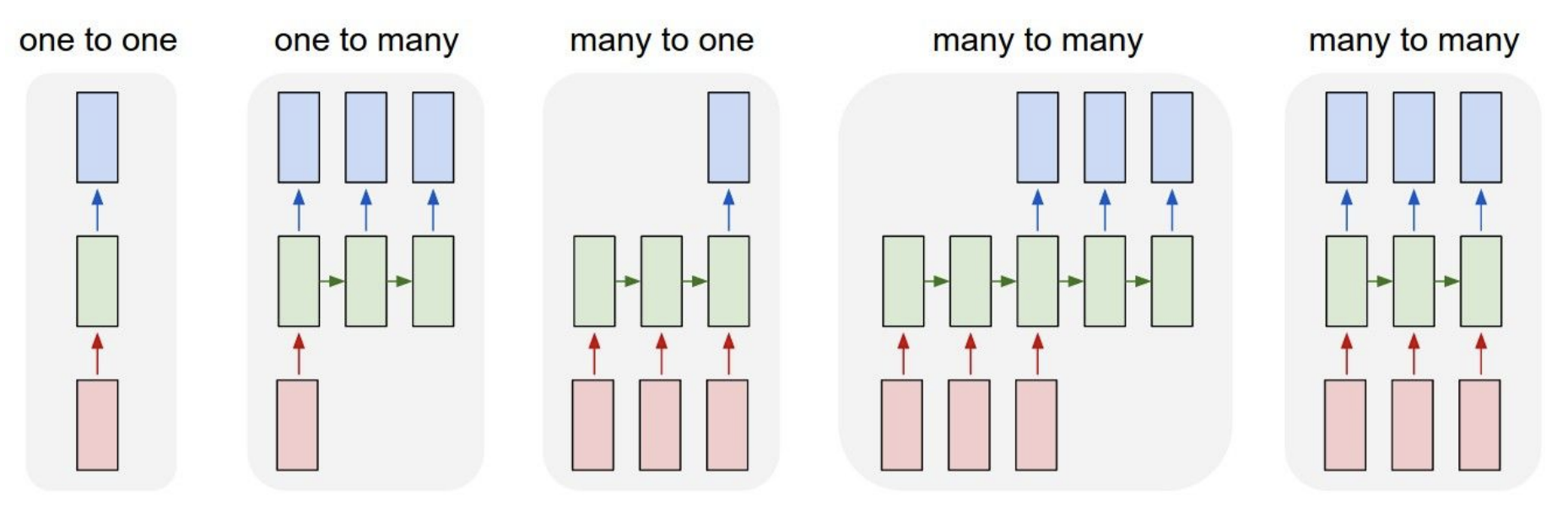
Reccurrent Equation#

\[ h_t = f(h_{t-1}, x_t) \]

$h_t$ is the hidden state at time $t$.
$h_{t-1}$ is the hidden state at time $t-1$.
$x_t$ is the input at time $t$.

Question

But, what do we do with these hidden states? We want to predict the next character in the sequence.

Answer

The reccurent equation just represents the “encoder”. We need a “decoder” to predict the next character in the sequence.

Encoder-Decoder#

Encoder ($f$): Encodes an input into a hidden state.
Decoder ($g$): Decodes the hidden state into an output.

Thought

This looks similar to vanilla neural network with one hidden layer. The hidden layer is encoding the input and the output layer is decoding the hidden state.

Answer

Yes, we can generelize “Encoder-Decoder” terminology to vanilla neural networks as well.

	Encoder	Decoder
Vanilla NNs	$h = f(x)$	$y = g(h)$
RNNs	$h_t = f(h_{t-1}, x_t)$	$y_t = g(h_t)$
Another way?	$h_{t-1} = f(x_{t-1})$	$y_t = g(h_{t-1}, x_t)$

Another way is related to Neural processes. Okay, back to the focus of this notebook.

Coding RNNs#

class RNNEncoder(nn.Module):
    def __init__(self, feat_dim: int, hidden_dim: int):
        super(RNNEncoder, self).__init__()
        self.w_x = nn.Parameter(torch.randn(feat_dim, hidden_dim) / np.sqrt(feat_dim * hidden_dim)) 
        self.w_h = nn.Parameter(torch.randn(hidden_dim, hidden_dim) / np.sqrt(hidden_dim * hidden_dim))
        self.b = nn.Parameter(torch.zeros(hidden_dim))
        
    @jaxtyped(typechecker=beartype)
    def forward(self, 
                x: Float[Tensor, "batch_dim feat_dim"], 
                h_prev: Union[Float[Tensor, "batch_dim hidden_dim"], None] = None
                ) -> Float[Tensor, "batch_dim hidden_dim"]:
        if h_prev is None:
            h = x @ self.w_x + self.b
        else:
            h = x @ self.w_x + h_prev @ self.w_h + self.b
        return F.relu(h)
    
class RNNDecoder(nn.Module):
    def __init__(self, hidden_dim: int, output_dim: int):
        super(RNNDecoder, self).__init__()
        self.w = nn.Parameter(torch.randn(hidden_dim, output_dim) / np.sqrt(hidden_dim * output_dim))
        self.b = nn.Parameter(torch.zeros(output_dim))
        
    @jaxtyped(typechecker=beartype)
    def forward(self, h: Float[Tensor, "batch_dim hidden_dim"]) -> Float[Tensor, "batch_dim output_dim"]:
        x = h @ self.w + self.b
        return x
    
class RNN(nn.Module):
    def __init__(self, feat_dim: int, hidden_dim: int, output_dim: int, sequence_len: int):
        super(RNN, self).__init__()
        self.encoder = RNNEncoder(feat_dim, hidden_dim)
        self.decoder = RNNDecoder(hidden_dim, output_dim)
        self.sequence_len = sequence_len
        self.hidden_dim = hidden_dim
        
    def forward(self, x: Float[Tensor, "batch_dim sequence_len feat_dim"]) -> Float[Tensor, "batch_dim feat_dim"]:
        self.h = None # initial hidden state
        
        # encode
        for seq_idx in range(1, self.sequence_len):
            self.h = self.encoder(x[:, seq_idx, :], self.h)
        
        # decode
        y_hat = self.decoder(self.h)
        return y_hat

Checking with dummy data#

tmp_batch_dim = 2
tmp_feat_dim = 3
tmp_output_dim = 7
tmp_hidden_dim = 5
tmp_sequence_len = 10
x = torch.randn(tmp_batch_dim, tmp_sequence_len, tmp_feat_dim)
model = RNN(tmp_feat_dim, tmp_hidden_dim, tmp_output_dim, tmp_sequence_len)
assert model(x).shape == (tmp_batch_dim, tmp_output_dim)

Getting some training data#

Let’s train the model on abstracts of multiple papers.

# import kaggle

# kaggle.api.dataset_download_files("Cornell-University/arxiv", path="data", unzip=True)

import json

with open("data/arxiv-metadata-oai-snapshot.json", "r") as f:
    data = []
    for i in range(100):
        data.append(json.loads(f.readline()))

vocab = set('\n'.join([d["abstract"] for d in data]))
len(vocab)

tokenizer = OneHotEncoder(sparse_output=False)
tokenizer.fit(np.array(list(vocab)).reshape(-1, 1))

OneHotEncoder(sparse_output=False)

In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

tokenizer.transform(np.array(["a", "b", "c"]).reshape(3, 1)).shape

(3, 93)

Create training sequences#

sequence_len = 20
inputs = []
outputs = []
for d in tqdm(data):
    abstract = d["abstract"].replace("\n", " ")
    for i in range(len(abstract) - sequence_len):
        input_seq = abstract[i:i+sequence_len]
        output_token = abstract[i+sequence_len]
        inputs.append(np.array(list(input_seq)))
        outputs.append(np.array(list(output_token)))
        
inputs = np.stack(inputs)
outputs = np.stack(outputs)
print(inputs.shape, outputs.shape)
inputs = tokenizer.transform(inputs.reshape(-1, 1)).reshape(inputs.shape[0], sequence_len, -1)
outputs = tokenizer.transform(outputs.reshape(-1, 1)).reshape(outputs.shape[0], -1)
print(inputs.shape, outputs.shape)

(78641, 20) (78641, 1)
(78641, 20, 93) (78641, 93)

Train the model#

batch_size = 512
epochs = 100
hidden_dim = 1024

train_inputs = inputs[:int(0.8*len(inputs))]
train_outputs = outputs[:int(0.8*len(outputs))]
test_inputs = inputs[int(0.8*len(inputs)):]
test_outputs = outputs[int(0.8*len(outputs)):]

dataset = TensorDataset(torch.tensor(train_inputs, dtype=torch.float32).to(device), torch.tensor(train_outputs, dtype=torch.float32).to(device))
dataloader = DataLoader(dataset, batch_size=batch_size, shuffle=True)

feat_dim = len(vocab)
output_dim = len(vocab)

model = RNN(feat_dim, hidden_dim, output_dim, sequence_len)
# model = torch.compile(model)
model.to(device)
optimizer = optim.Adam(model.parameters(), lr=1e-4)

iter_losses = []
epoch_losses = []
pbar = tqdm(range(epochs))
for epoch in pbar:
    loss_accum = 0
    for x, y in dataloader:
        y_hat = model(x)
        loss = F.cross_entropy(y_hat, y.argmax(dim=1))
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        iter_losses.append(loss.item())
        loss_accum += loss.item()
    epoch_losses.append(loss_accum / len(dataloader))
    pbar.set_postfix({"loss": epoch_losses[-1]})

pbar = tqdm(range(20))
model.train()
for epoch in pbar:
    loss_accum = 0
    for x, y in dataloader:
        y_hat = model(x)
        loss = F.cross_entropy(y_hat, y.argmax(dim=1))
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        iter_losses.append(loss.item())
        loss_accum += loss.item()
    epoch_losses.append(loss_accum / len(dataloader))
    pbar.set_postfix({"loss": epoch_losses[-1]})

Generate text#

def get_char(y_hat):
    y_hat_cat = torch.zeros(y_hat.shape)
    pred_idx = y_hat.argmax(dim=1)
    y_hat_cat[:, pred_idx] = 1
    pred_char = tokenizer.inverse_transform(y_hat_cat)
    return y_hat_cat, pred_char.item()

def generator(model, input_seq, generated_len):
    model.eval()
    with torch.no_grad():
        gen_chars = []
        for i in range(generated_len):
            y_hat = model(input_seq)
            y_hat_cat, pred_char = get_char(y_hat)
            
            # print(input_seq.shape, y_hat_cat.shape)
            input_seq = torch.cat([input_seq[:, 1:, :], y_hat_cat[None, ...].to(device)], dim=1)
            
            one_idx = y_hat.numpy(force=True).argmax()
            pred = np.zeros(y_hat.shape)
            # print(pred.shape)
            pred[:, one_idx] = 1
            pred_char = tokenizer.inverse_transform(pred)
            gen_chars.append(pred_char.item())
            
    return "".join(gen_chars)

# input
idx = 500
try_input = test_inputs[idx:idx+1]
print("Input:")
print("".join(tokenizer.inverse_transform(try_input[0]).reshape(-1)))

print("\nOutput:")
print(generator(model, torch.tensor(try_input, dtype=torch.float32).to(device), 200))

Input:
right solitons under

Output:
edina in approxistibg inctian strgenslis crmporibnt whew itecharizn pust becala inemantwond the $imile an Paksu foundtion, finitlerans ard dousculaca. The possting of the derev. Thi s)steed s. Te  aen

Long Short-Term Memory (LSTM)#

RNNs have vanishing gradient problem. LSTM is a solution to this problem.

	Encoder	Decoder
Vanilla NNs	$h = f(x)$	$y = g(h)$
RNNs	$h_t = f(h_{t-1}, x_t)$	$y_t = g(h_t)$

For LSTM

Encoder

(37)#\[\begin{align} \text{Forget: } & f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f) \\ \text{Input: } & i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i) \\ \text{Output: } & o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o) \\ \text{Cell: } & \tilde{C}_t = \tanh(W_C \cdot [h_{t-1}, x_t] + b_C) \\ \text{Cell state: } & C_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_t \\ \text{Hidden state: } & h_t = o_t \odot \tanh(C_t) \end{align}\]

Decoder $$ y_t = g(h_t) $$

Coding LSTMs#

class LSTMEncoder(nn.Module):
    def __init__(self, feat_dim: int, hidden_dim: int):
        super(LSTMEncoder, self).__init__()
        def get_weights():
            w_x = nn.Parameter(torch.randn(feat_dim, hidden_dim) / np.sqrt(feat_dim * hidden_dim))
            w_h = nn.Parameter(torch.randn(hidden_dim, hidden_dim) / np.sqrt(hidden_dim * hidden_dim))
            b = nn.Parameter(torch.zeros(hidden_dim))
            return w_x, w_h, b
        
        # forget gate
        self.w_x_f, self.w_h_f, self.b_f = get_weights()
        
        # input gate
        self.w_x_i, self.w_h_i, self.b_i = get_weights()
        
        # output gate
        self.w_x_o, self.w_h_o, self.b_o = get_weights()
        
        # cell weights
        self.w_x_c, self.w_h_c, self.b_c = get_weights()
        
    @jaxtyped(typechecker=beartype)
    def forward(self, 
                x: Float[Tensor, "batch_dim feat_dim"], 
                h_prev: Float[Tensor, "batch_dim hidden_dim"] = None,
                c_prev: Float[Tensor, "batch_dim hidden_dim"] = None,
                ) -> Tuple[Float[Tensor, "batch_dim hidden_dim"], Float[Tensor, "batch_dim hidden_dim"]]:
        if h_prev is None:
            i_t = torch.sigmoid(x @ self.w_x_i + self.b_i) # input multiplier
            o_t = torch.sigmoid(x @ self.w_x_o + self.b_o) # output multiplier
            c_t = torch.tanh(x @ self.w_x_c + self.b_c) # pre cell state
            c_t = i_t * c_t # cell state
            h_t = o_t * torch.tanh(c_t) # hidden state
        else:
            f_t = torch.sigmoid(x @ self.w_x_f + h_prev @ self.w_h_f + self.b_f) # forget gate
            i_t = torch.sigmoid(x @ self.w_x_i + h_prev @ self.w_h_i + self.b_i) # input multiplier
            o_t = torch.sigmoid(x @ self.w_x_o + h_prev @ self.w_h_o + self.b_o) # output multiplier
            c_t = torch.tanh(x @ self.w_x_c + h_prev @ self.w_h_c + self.b_c) # pre cell state
            c_t = i_t * c_t + f_t * c_prev # cell state
            h_t = o_t * torch.tanh(c_t) # hidden state
        
        return (h_t, c_t)
    
class LSTM(nn.Module):
    def __init__(self, feat_dim: int, hidden_dim: int, output_dim: int, sequence_len: int):
        super(LSTM, self).__init__()
        self.encoder = LSTMEncoder(feat_dim, hidden_dim)
        self.decoder = RNNDecoder(hidden_dim, output_dim)
        
    @jaxtyped(typechecker=beartype)
    def forward(self, x: Float[Tensor, "batch_dim sequence_len feat_dim"]) -> Float[Tensor, "batch_dim output_dim"]:
        h, c = self.encoder(x[:, 0, :])
        for seq_idx in range(1, x.shape[1]):
            h, c = self.encoder(x[:, seq_idx, :], h, c)
        y_hat = self.decoder(h)
        return y_hat

batch_size = 512
epochs = 100
hidden_dim = 1024

model = LSTM(feat_dim, hidden_dim, output_dim, sequence_len)
# model = torch.compile(model)
model.to(device)
optimizer = optim.Adam(model.parameters(), lr=1e-3)
# optimizer = optim.SGD(model.parameters(), lr=1e-3, momentum=0.9)

iter_losses = []
epoch_losses = []
pbar = tqdm(range(epochs))
for epoch in pbar:
    loss_accum = 0
    for x, y in dataloader:
        y_hat = model(x)
        loss = F.cross_entropy(y_hat, y.argmax(dim=1))
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
        iter_losses.append(loss.item())
        loss_accum += loss.item()
    epoch_losses.append(loss_accum / len(dataloader))
    pbar.set_postfix({"loss": epoch_losses[-1]})

def get_char(y_hat):
    y_hat_cat = torch.zeros(y_hat.shape)
    pred_idx = y_hat.argmax(dim=1)
    y_hat_cat[:, pred_idx] = 1
    pred_char = tokenizer.inverse_transform(y_hat_cat)
    return y_hat_cat, pred_char.item()

def generator(model, input_seq, generated_len):
    model.eval()
    with torch.no_grad():
        gen_chars = []
        for i in range(generated_len):
            y_hat = model(input_seq)
            y_hat_cat, pred_char = get_char(y_hat)
            
            # print(input_seq.shape, y_hat_cat.shape)
            input_seq = torch.cat([input_seq[:, 1:, :], y_hat_cat[None, ...].to(device)], dim=1)
            
            one_idx = y_hat.numpy(force=True).argmax()
            pred = np.zeros(y_hat.shape)
            # print(pred.shape)
            pred[:, one_idx] = 1
            pred_char = tokenizer.inverse_transform(pred)
            gen_chars.append(pred_char.item())
            
    return "".join(gen_chars)

# input
idx = 1200
try_input = test_inputs[idx:idx+1]
print("Input:")
input_text = "".join(tokenizer.inverse_transform(try_input[0]).reshape(-1))
print(input_text)

print("\nOutput:")
gen_text = generator(model, torch.tensor(try_input, dtype=torch.float32).to(device), 300)
print(input_text + gen_text)

Input:
ant. Inflationary co

Output:
ant. Inflationary conditions. The resulting soliton solutions can be regarded as a generalization of the method. Finally, the position of the DDA among other methods of light scattering by very large particles, like the ones that are considered in this manuscript. Current limitations and possible ways for improvement a

	Encoder	Decoder
Vanilla NNs	\(h = f(x)\)	\(y = g(h)\)
RNNs	\(h_t = f(h_{t-1}, x_t)\)	\(y_t = g(h_t)\)
Another way?	\(h_{t-1} = f(x_{t-1})\)	\(y_t = g(h_{t-1}, x_t)\)