Contents
import GPy
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
import numpy as np
true_kernel_lengthscale = 2.0
true_kernel_variance = 1.0
true_noise = 0.5
kernel = GPy.kern.RBF(
input_dim=1, variance=true_kernel_variance, lengthscale=true_kernel_lengthscale
)
kernel
| rbf. | value | constraints | priors |
|---|---|---|---|
| variance | 1.0 | +ve | |
| lengthscale | 2.0 | +ve |
X = np.linspace(-4.0, 4.0, 250)[:, None]
C = kernel.K(X, X)
np.random.seed(0)
f = np.random.multivariate_normal(np.zeros_like(X.flatten()), C)
noise = np.random.normal(loc=0, scale=true_noise, size=f.flatten().size)
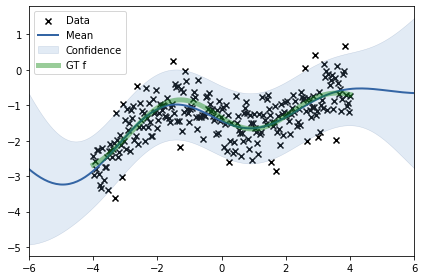
plt.plot(X, f, lw=5)
plt.scatter(X, f + noise, s=20, alpha=0.4, c="k")
<matplotlib.collections.PathCollection at 0x1260edac0>
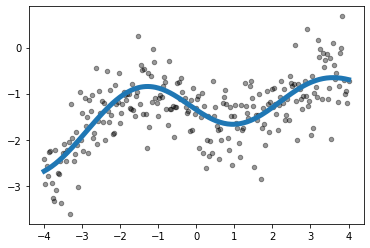
k = GPy.kern.RBF(input_dim=1)
m = GPy.models.GPRegression(X, (f + noise).reshape(-1, 1), k)
m.plot()
{'dataplot': [<matplotlib.collections.PathCollection at 0x1261f6d60>],
'gpmean': [[<matplotlib.lines.Line2D at 0x1262092b0>]],
'gpconfidence': [<matplotlib.collections.PolyCollection at 0x1261e8d30>]}
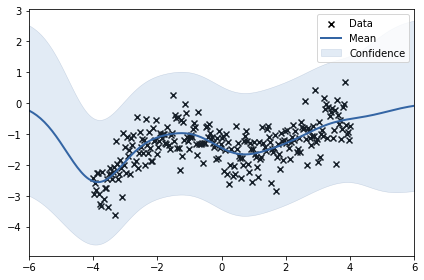
_ = m.optimize_restarts()
Optimization restart 1/10, f = 195.84754738377032
Optimization restart 2/10, f = 195.84754738420352
Optimization restart 3/10, f = 195.84754738488476
Optimization restart 4/10, f = 195.84754738373357
Optimization restart 5/10, f = 195.84754738844853
Optimization restart 6/10, f = 195.84754738371487
Optimization restart 7/10, f = 195.847547383823
Optimization restart 8/10, f = 195.84754738461945
Optimization restart 9/10, f = 195.84754738372928
Optimization restart 10/10, f = 195.84754738422166
m
Model: GP regression
Objective: 195.84754738371487
Number of Parameters: 3
Number of Optimization Parameters: 3
Updates: True
| GP_regression. | value | constraints | priors |
|---|---|---|---|
| rbf.variance | 3.173279047762375 | +ve | |
| rbf.lengthscale | 2.3422120232188184 | +ve | |
| Gaussian_noise.variance | 0.25032019995651095 | +ve |
k = GPy.kern.RBF(
input_dim=1, variance=true_kernel_variance, lengthscale=true_kernel_lengthscale
)
m = GPy.models.GPRegression(X, (f + noise).reshape(-1, 1), k)
m.optimize_restarts()
Optimization restart 1/10, f = 195.8475473936342
Optimization restart 2/10, f = 195.84754738474803
Optimization restart 3/10, f = 195.84754754618757
Optimization restart 4/10, f = 195.84754738374266
Optimization restart 5/10, f = 195.84754738772745
Optimization restart 6/10, f = 195.84754738398067
Optimization restart 7/10, f = 195.84754738390444
Optimization restart 8/10, f = 195.84754738371876
Optimization restart 9/10, f = 195.8475473837782
Optimization restart 10/10, f = 195.8475473893405
[<paramz.optimization.optimization.opt_lbfgsb at 0x126264e50>,
<paramz.optimization.optimization.opt_lbfgsb at 0x126276d30>,
<paramz.optimization.optimization.opt_lbfgsb at 0x126276490>,
<paramz.optimization.optimization.opt_lbfgsb at 0x1261215e0>,
<paramz.optimization.optimization.opt_lbfgsb at 0x12615cc10>,
<paramz.optimization.optimization.opt_lbfgsb at 0x12615c460>,
<paramz.optimization.optimization.opt_lbfgsb at 0x126243d00>,
<paramz.optimization.optimization.opt_lbfgsb at 0x1261bbd90>,
<paramz.optimization.optimization.opt_lbfgsb at 0x1262760d0>,
<paramz.optimization.optimization.opt_lbfgsb at 0x126264310>]
m
Model: GP regression
Objective: 195.84754738371876
Number of Parameters: 3
Number of Optimization Parameters: 3
Updates: True
| GP_regression. | value | constraints | priors |
|---|---|---|---|
| rbf.variance | 3.173275150587815 | +ve | |
| rbf.lengthscale | 2.342210766061685 | +ve | |
| Gaussian_noise.variance | 0.2503201961365106 | +ve |
m.plot()
plt.plot(X, f, lw=5, label="GT f", alpha=0.4, color='green')
plt.legend()
<matplotlib.legend.Legend at 0x1262b6d60>