Maximum Likelihood Estimation (MLE) for parameters of univariate and multivariate normal distribution in PyTorch
Contents
Maximum Likelihood Estimation (MLE) for parameters of univariate and multivariate normal distribution in PyTorch¶
import torch
import seaborn as sns
import pandas as pd
import matplotlib.pyplot as plt
sns.reset_defaults()
sns.set_context(context="talk", font_scale=1)
%matplotlib inline
%config InlineBackend.figure_format='retina'
dist = torch.distributions
Creating a 1d normal distribution¶
uv_normal = dist.Normal(loc=0.0, scale=1.0)
Sampling from the distribution¶
samples = uv_normal.sample(sample_shape=[1000])
sns.histplot(samples)
sns.despine()
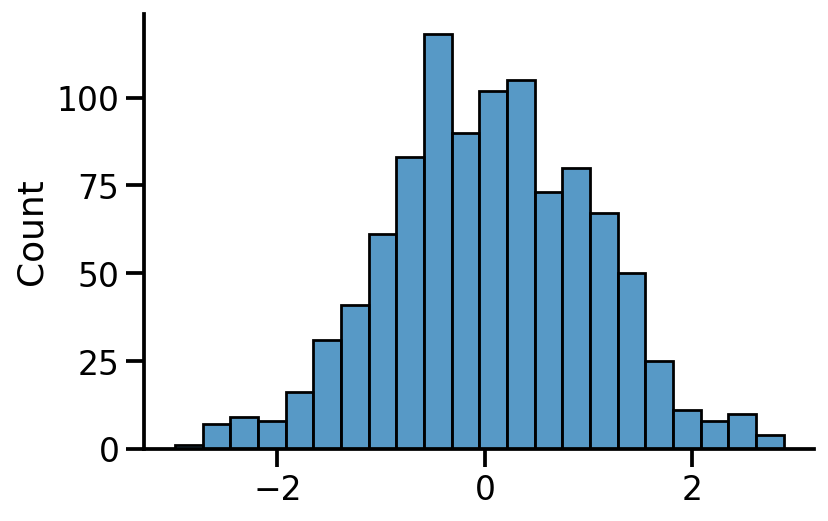
sns.kdeplot(samples, bw_adjust=2)
sns.despine()
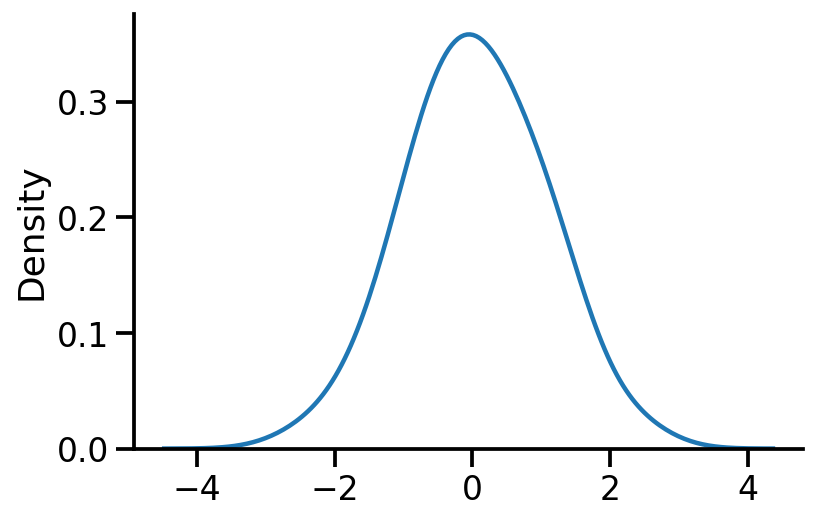
Computing logprob and prob at a given x¶
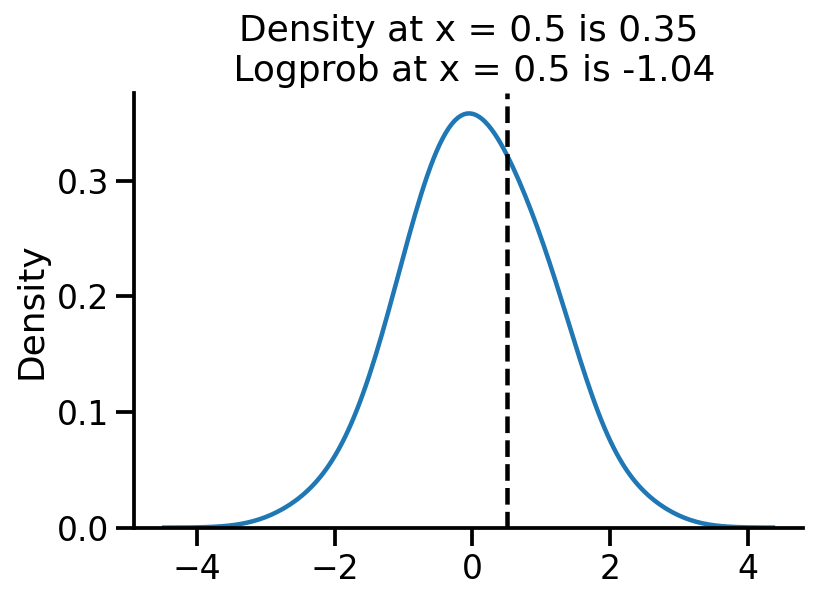
sns.kdeplot(samples, bw_adjust=2)
plt.axvline(0.5, color="k", linestyle="--")
log_pdf_05 = uv_normal.log_prob(torch.Tensor([0.5]))
pdf_05 = torch.exp(log_pdf_05)
plt.title(
"Density at x = 0.5 is {:.2f}\n Logprob at x = 0.5 is {:.2f}".format(
pdf_05.numpy()[0], log_pdf_05.numpy()[0]
)
)
sns.despine()
Learning parameters via MLE¶
Let us generate some normally distributed data and see if we can learn the mean.
train_data = uv_normal.sample([10000])
uv_normal.loc, uv_normal.scale
(tensor(0.), tensor(1.))
train_data.mean(), train_data.std()
(tensor(-0.0174), tensor(1.0049))
The above is the analytical MLE solution
Setting 1: Fixed scale, learning only location¶
loc = torch.tensor(-10.0, requires_grad=True)
opt = torch.optim.Adam([loc], lr=0.01)
for i in range(3100):
to_learn = torch.distributions.Normal(loc=loc, scale=1.0)
loss = -torch.sum(to_learn.log_prob(train_data))
loss.backward()
if i % 500 == 0:
print(f"Iteration: {i}, Loss: {loss.item():0.2f}, Loc: {loc.item():0.2f}")
opt.step()
opt.zero_grad()
Iteration: 0, Loss: 512500.16, Loc: -10.00
Iteration: 500, Loss: 170413.53, Loc: -5.61
Iteration: 1000, Loss: 47114.50, Loc: -2.58
Iteration: 1500, Loss: 18115.04, Loc: -0.90
Iteration: 2000, Loss: 14446.38, Loc: -0.22
Iteration: 2500, Loss: 14242.16, Loc: -0.05
Iteration: 3000, Loss: 14238.12, Loc: -0.02
print(
f"MLE location gradient descent: {loc:0.2f}, MLE location analytical: {train_data.mean().item():0.2f}"
)
MLE location gradient descent: -0.02, MLE location analytical: -0.02
Setting 2: Learning location and scale¶
An important difference from the previous code is that we need to use a transformed variable to ensure scale is positive. We do so by using softplus.
loc = torch.tensor(-10.0, requires_grad=True)
scale = torch.tensor(2.0, requires_grad=True)
opt = torch.optim.Adam([loc, scale], lr=0.01)
for i in range(5100):
scale_softplus = torch.functional.F.softplus(scale)
to_learn = torch.distributions.Normal(loc=loc, scale=scale_softplus)
loss = -torch.sum(to_learn.log_prob(train_data))
loss.backward()
if i % 500 == 0:
print(
f"Iteration: {i}, Loss: {loss.item():0.2f}, Loc: {loc.item():0.2f}, Scale: {scale_softplus.item():0.2f}"
)
opt.step()
opt.zero_grad()
Iteration: 0, Loss: 127994.02, Loc: -10.00, Scale: 2.13
Iteration: 500, Loss: 37320.10, Loc: -6.86, Scale: 4.15
Iteration: 1000, Loss: 29944.32, Loc: -4.73, Scale: 4.59
Iteration: 1500, Loss: 26326.08, Loc: -2.87, Scale: 4.37
Iteration: 2000, Loss: 22592.90, Loc: -1.19, Scale: 3.46
Iteration: 2500, Loss: 15968.47, Loc: -0.06, Scale: 1.63
Iteration: 3000, Loss: 14237.87, Loc: -0.02, Scale: 1.01
Iteration: 3500, Loss: 14237.87, Loc: -0.02, Scale: 1.00
Iteration: 4000, Loss: 14237.87, Loc: -0.02, Scale: 1.00
Iteration: 4500, Loss: 14237.87, Loc: -0.02, Scale: 1.00
Iteration: 5000, Loss: 14237.87, Loc: -0.02, Scale: 1.00
print(
f"MLE loc gradient descent: {loc:0.2f}, MLE loc analytical: {train_data.mean().item():0.2f}"
)
print(
f"MLE scale gradient descent: {scale_softplus:0.2f}, MLE scale analytical: {train_data.std().item():0.2f}"
)
MLE loc gradient descent: -0.02, MLE loc analytical: -0.02
MLE scale gradient descent: 1.00, MLE scale analytical: 1.00
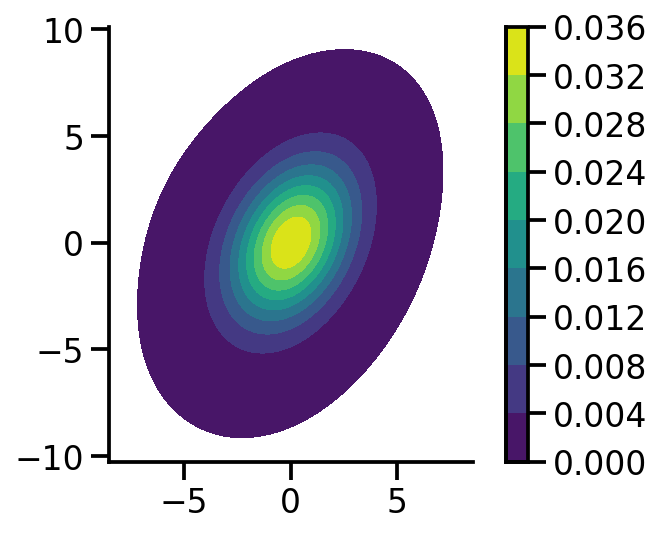
mvn = dist.MultivariateNormal(
loc=torch.zeros(2), covariance_matrix=torch.tensor([[1.0, 0.5], [0.5, 2.0]])
)
mvn_samples = mvn.sample([1000])
sns.kdeplot(
x=mvn_samples[:, 0],
y=mvn_samples[:, 1],
zorder=0,
n_levels=10,
shade=True,
cbar=True,
thresh=0.001,
cmap="viridis",
bw_adjust=5,
cbar_kws={
"format": "%.3f",
},
)
plt.gca().set_aspect("equal")
sns.despine()
Setting 1: Fixed scale, learning only location¶
loc = torch.tensor([-10.0, 5.0], requires_grad=True)
opt = torch.optim.Adam([loc], lr=0.01)
for i in range(4100):
to_learn = dist.MultivariateNormal(
loc=loc, covariance_matrix=torch.tensor([[1.0, 0.5], [0.5, 2.0]])
)
loss = -torch.sum(to_learn.log_prob(mvn_samples))
loss.backward()
if i % 500 == 0:
print(f"Iteration: {i}, Loss: {loss.item():0.2f}, Loc: {loc}")
opt.step()
opt.zero_grad()
Iteration: 0, Loss: 81817.08, Loc: tensor([-10., 5.], requires_grad=True)
Iteration: 500, Loss: 23362.23, Loc: tensor([-5.6703, 0.9632], requires_grad=True)
Iteration: 1000, Loss: 7120.20, Loc: tensor([-2.7955, -0.8165], requires_grad=True)
Iteration: 1500, Loss: 3807.52, Loc: tensor([-1.1763, -0.8518], requires_grad=True)
Iteration: 2000, Loss: 3180.41, Loc: tensor([-0.4009, -0.3948], requires_grad=True)
Iteration: 2500, Loss: 3093.31, Loc: tensor([-0.0965, -0.1150], requires_grad=True)
Iteration: 3000, Loss: 3087.07, Loc: tensor([-0.0088, -0.0259], requires_grad=True)
Iteration: 3500, Loss: 3086.89, Loc: tensor([ 0.0073, -0.0092], requires_grad=True)
Iteration: 4000, Loss: 3086.88, Loc: tensor([ 0.0090, -0.0075], requires_grad=True)
loc, mvn_samples.mean(axis=0)
(tensor([ 0.0090, -0.0075], requires_grad=True), tensor([ 0.0090, -0.0074]))
We can see that our approach yields the same results as the analytical MLE
Setting 2: Learning scale and location¶
We need to now choose the equivalent of standard deviation in MVN case, this is the Cholesky matrix which should be a lower triangular matrix
loc = torch.tensor([-10.0, 5.0], requires_grad=True)
tril = torch.autograd.Variable(torch.tril(torch.ones(2, 2)), requires_grad=True)
opt = torch.optim.Adam([loc, tril], lr=0.01)
for i in range(8100):
to_learn = dist.MultivariateNormal(loc=loc, covariance_matrix=tril @ tril.t())
loss = -torch.sum(to_learn.log_prob(mvn_samples))
loss.backward()
if i % 500 == 0:
print(f"Iteration: {i}, Loss: {loss.item():0.2f}, Loc: {loc}")
opt.step()
opt.zero_grad()
Iteration: 0, Loss: 166143.42, Loc: tensor([-10., 5.], requires_grad=True)
Iteration: 500, Loss: 9512.82, Loc: tensor([-7.8985, 3.2943], requires_grad=True)
Iteration: 1000, Loss: 6411.09, Loc: tensor([-6.4121, 2.5011], requires_grad=True)
Iteration: 1500, Loss: 5248.90, Loc: tensor([-5.0754, 1.8893], requires_grad=True)
Iteration: 2000, Loss: 4647.84, Loc: tensor([-3.8380, 1.3627], requires_grad=True)
Iteration: 2500, Loss: 4289.96, Loc: tensor([-2.6974, 0.9030], requires_grad=True)
Iteration: 3000, Loss: 4056.93, Loc: tensor([-1.6831, 0.5176], requires_grad=True)
Iteration: 3500, Loss: 3885.87, Loc: tensor([-0.8539, 0.2273], requires_grad=True)
Iteration: 4000, Loss: 3722.92, Loc: tensor([-0.2879, 0.0543], requires_grad=True)
Iteration: 4500, Loss: 3495.34, Loc: tensor([-0.0310, -0.0046], requires_grad=True)
Iteration: 5000, Loss: 3145.29, Loc: tensor([ 0.0089, -0.0075], requires_grad=True)
Iteration: 5500, Loss: 3080.54, Loc: tensor([ 0.0090, -0.0074], requires_grad=True)
Iteration: 6000, Loss: 3080.53, Loc: tensor([ 0.0090, -0.0074], requires_grad=True)
Iteration: 6500, Loss: 3080.53, Loc: tensor([ 0.0090, -0.0074], requires_grad=True)
Iteration: 7000, Loss: 3080.53, Loc: tensor([ 0.0090, -0.0074], requires_grad=True)
Iteration: 7500, Loss: 3080.53, Loc: tensor([ 0.0090, -0.0074], requires_grad=True)
Iteration: 8000, Loss: 3080.53, Loc: tensor([ 0.0090, -0.0074], requires_grad=True)
to_learn.loc, to_learn.covariance_matrix
(tensor([ 0.0090, -0.0074], grad_fn=<AsStridedBackward0>),
tensor([[1.0582, 0.4563],
[0.4563, 1.7320]], grad_fn=<ExpandBackward0>))
mle_loc = mvn_samples.mean(axis=0)
mle_loc
tensor([ 0.0090, -0.0074])
mle_covariance = (
(mvn_samples - mle_loc).t() @ ((mvn_samples - mle_loc)) / mvn_samples.shape[0]
)
mle_covariance
tensor([[1.0582, 0.4563],
[0.4563, 1.7320]])
We can see that our gradient based methods parameters match those of the MLE computed analytically.
References
