Logistic Regression using PyTorch distributions

Contents

Logistic Regression using PyTorch distributions¶

Basic Imports¶

import numpy as np
import matplotlib.pyplot as plt
import torch
import seaborn as sns
import pandas as pd

dist =torch.distributions

sns.reset_defaults()
sns.set_context(context="talk", font_scale=1)
%matplotlib inline
%config InlineBackend.figure_format='retina'

Generative model for logistic regression¶

x = dist.Normal(loc = torch.tensor([0., 0.]), scale=torch.tensor([1., 2.]))
x_sample = x.sample([100])
x_sample.shape

x_dash = torch.concat((torch.ones(x_sample.shape[0], 1), x_sample), axis=1)

theta = dist.MultivariateNormal(loc = torch.tensor([0., 0., 0.]), covariance_matrix=0.5*torch.eye(3))
theta_sample = theta.sample()

p = torch.sigmoid(x_dash@theta_sample)

y = dist.Bernoulli(probs=p)
y_sample = y.sample()

plt.scatter(x_sample[:, 0], x_sample[:, 1], c = y_sample, s=40, alpha=0.5)
sns.despine()

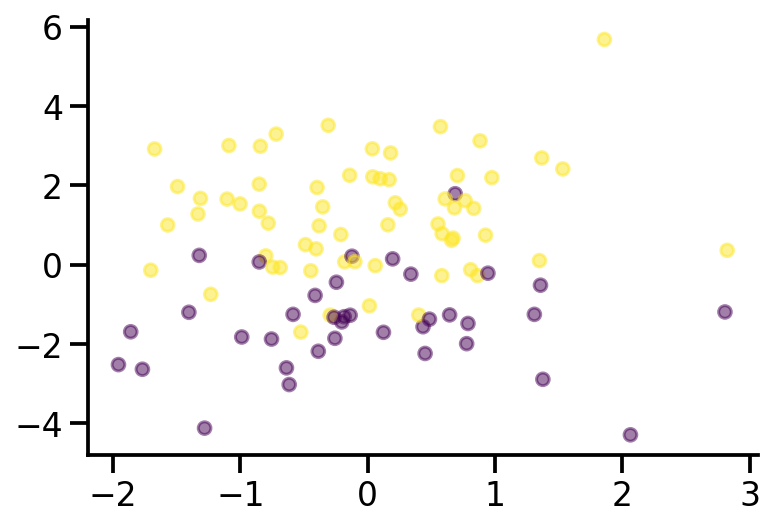
../../_images/2022-02-14-logistic-regression_6_0.png

theta_sample

tensor([ 0.6368, -0.7526,  1.4652])

from sklearn.linear_model import LogisticRegression
lr_l2 = LogisticRegression()
lr_none = LogisticRegression(penalty='none')

lr_l2.fit(x_sample, y_sample)
lr_none.fit(x_sample, y_sample)

LogisticRegression(penalty='none')

def plot_fit(x_sample, y_sample, theta, model_name):

    
    # Retrieve the model parameters.
    b = theta[0]
    w1, w2 = theta[1], theta[2]
    # Calculate the intercept and gradient of the decision boundary.
    c = -b/w2
    m = -w1/w2

    # Plot the data and the classification with the decision boundary.
    xmin, xmax = x_sample[:, 0].min()-0.2, x_sample[:, 0].max()+0.2
    ymin, ymax =  x_sample[:, 1].min()-0.2, x_sample[:, 1].max()+0.2
    xd = np.array([xmin, xmax])
    yd = m*xd + c
    plt.plot(xd, yd, 'k', lw=1, ls='--')
    plt.fill_between(xd, yd, ymin, color='tab:blue', alpha=0.2)
    plt.fill_between(xd, yd, ymax, color='tab:orange', alpha=0.2)

    plt.scatter(*x_sample[y_sample==0].T, s=20, alpha=0.5)
    plt.scatter(*x_sample[y_sample==1].T, s=20, alpha=0.5)
    plt.xlim(xmin, xmax)
    plt.ylim(ymin, ymax)
    plt.ylabel(r'$x_2$')
    plt.xlabel(r'$x_1$')
    theta_print = np.round(theta, 1)
    plt.title(f"{model_name}\n{theta_print}")
    sns.despine()

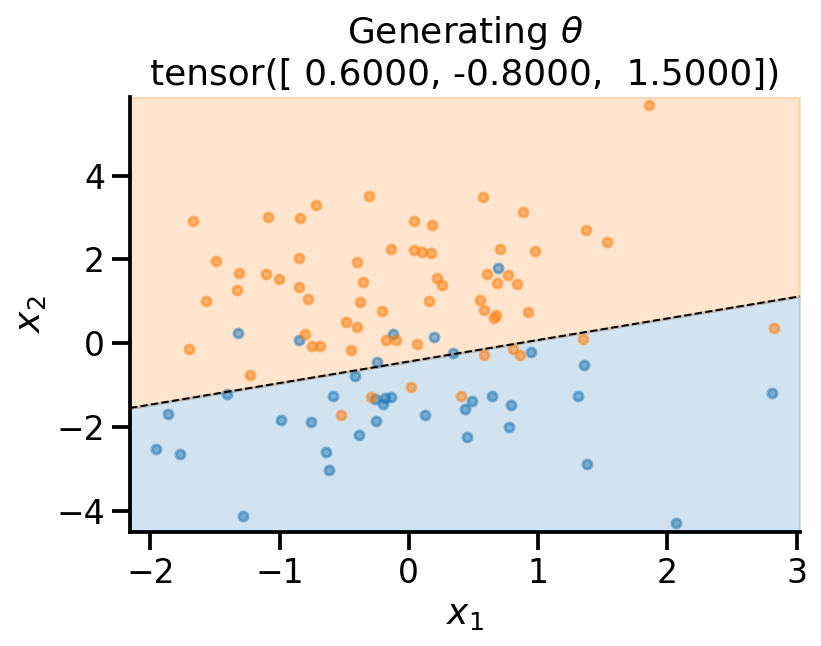
plot_fit(
    x_sample,
    y_sample,
    theta_sample,
    r"Generating $\theta$",
)

../../_images/2022-02-14-logistic-regression_11_0.png

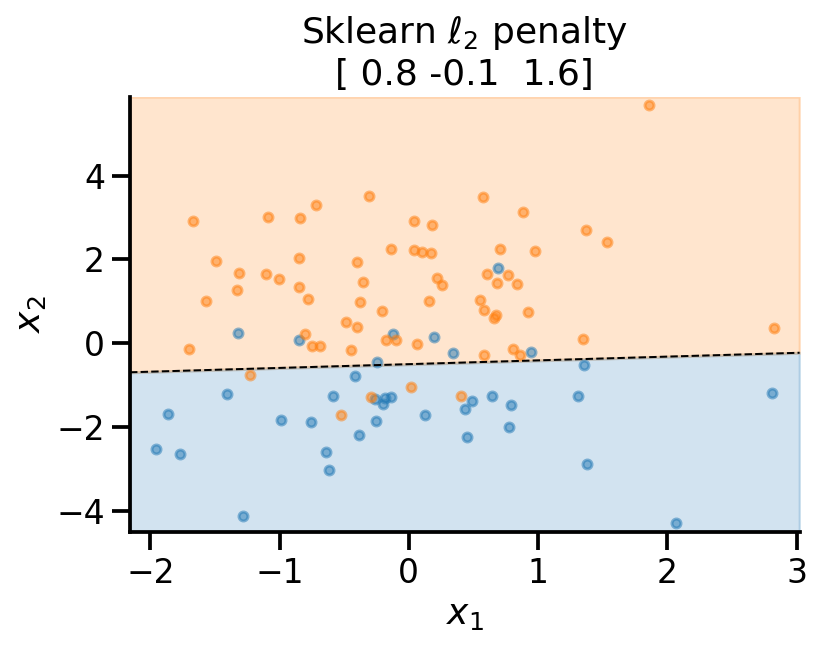
plot_fit(
    x_sample,
    y_sample,
    np.concatenate((lr_l2.intercept_.reshape(-1, 1), lr_l2.coef_), axis=1).flatten(),
    r"Sklearn $\ell_2$ penalty ",
)

../../_images/2022-02-14-logistic-regression_12_0.png

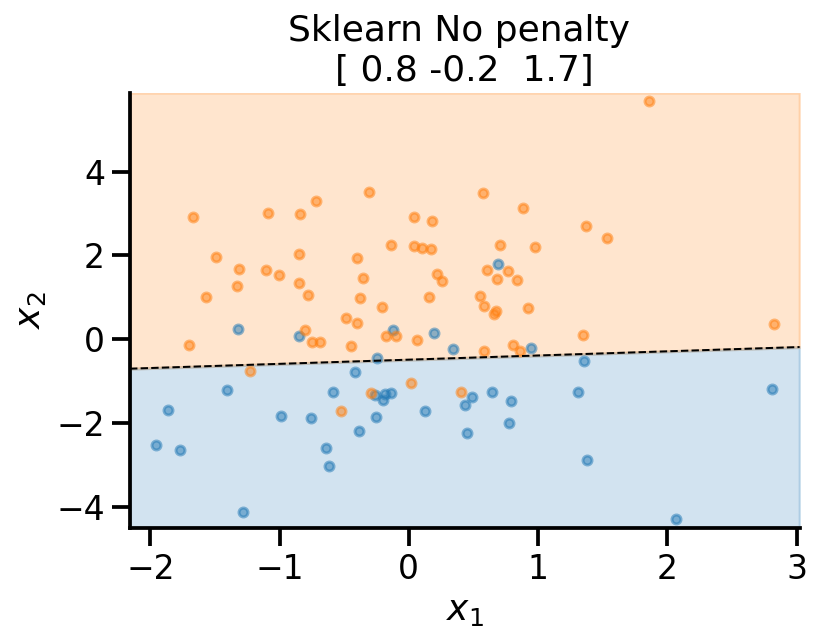
plot_fit(
    x_sample,
    y_sample,
    np.concatenate((lr_none.intercept_.reshape(-1, 1), lr_none.coef_), axis=1).flatten(),
    r"Sklearn No penalty ",
)

../../_images/2022-02-14-logistic-regression_13_0.png

MLE estimate PyTorch¶

def neg_log_likelihood(theta, x, y):
    x_dash = torch.concat((torch.ones(x.shape[0], 1), x), axis=1)
    p = torch.sigmoid(x_dash@theta)
    y_dist = dist.Bernoulli(probs=p)

    return -torch.sum(y_dist.log_prob(y))

neg_log_likelihood(theta_sample, x_sample, y_sample)

tensor(33.1907)

theta_learn_loc = torch.tensor([1., 1., 1.], requires_grad=True)
neg_log_likelihood(theta_learn_loc, x_sample, y_sample)

plot_fit(
    x_sample,
    y_sample,
    theta_learn_loc.detach(),
    r"Torch without training",
)

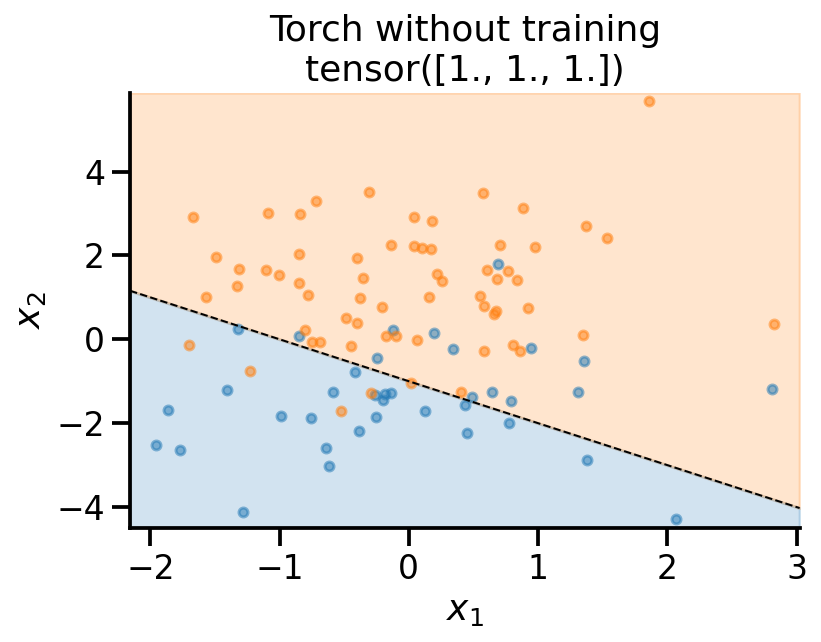
../../_images/2022-02-14-logistic-regression_17_0.png

theta_learn_loc = torch.tensor([0., 0., 0.], requires_grad=True)
loss_array = []
loc_array = []

opt = torch.optim.Adam([theta_learn_loc], lr=0.05)
for i in range(101):
    loss_val = neg_log_likelihood(theta_learn_loc, x_sample, y_sample)
    loss_val.backward()
    loc_array.append(theta_learn_loc)
    loss_array.append(loss_val.item())

    if i % 10 == 0:
        print(
            f"Iteration: {i}, Loss: {loss_val.item():0.2f}"
        )
    opt.step()
    opt.zero_grad()

Iteration: 0, Loss: 69.31
Iteration: 10, Loss: 44.14
Iteration: 20, Loss: 35.79
Iteration: 30, Loss: 32.73
Iteration: 40, Loss: 31.67
Iteration: 50, Loss: 31.25
Iteration: 60, Loss: 31.08
Iteration: 70, Loss: 31.00
Iteration: 80, Loss: 30.97
Iteration: 90, Loss: 30.95
Iteration: 100, Loss: 30.94

plot_fit(
    x_sample,
    y_sample,
    theta_learn_loc.detach(),
    r"Torch MLE",
)

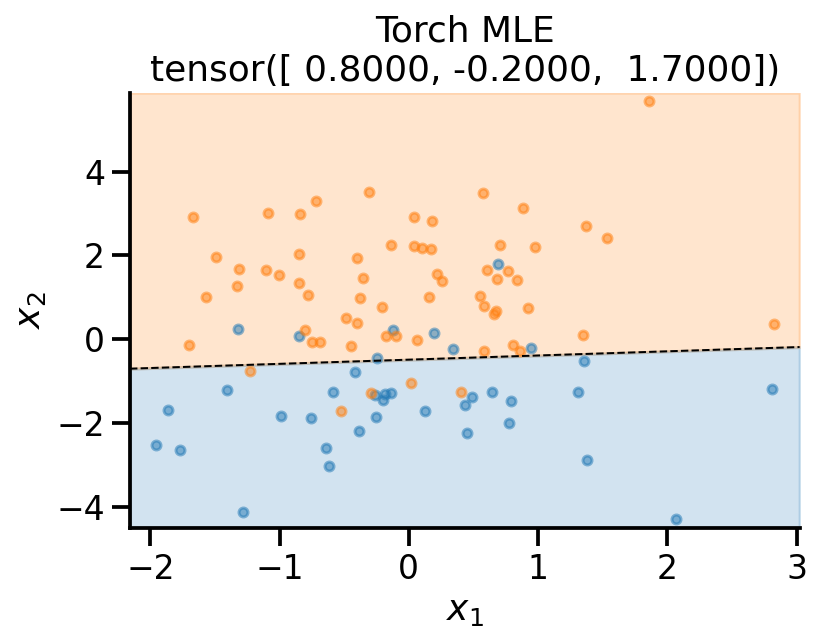
../../_images/2022-02-14-logistic-regression_19_0.png

MAP estimate PyTorch¶

prior_theta = dist.MultivariateNormal(loc = torch.tensor([0., 0., 0.]), covariance_matrix=2*torch.eye(3))

logprob = lambda theta: -prior_theta.log_prob(theta)

theta_learn_loc = torch.tensor([0., 0., 0.], requires_grad=True)
loss_array = []
loc_array = []

opt = torch.optim.Adam([theta_learn_loc], lr=0.05)
for i in range(101):
    loss_val = neg_log_likelihood(theta_learn_loc, x_sample, y_sample) + logprob(theta_learn_loc)
    loss_val.backward()
    loc_array.append(theta_learn_loc)
    loss_array.append(loss_val.item())

    if i % 10 == 0:
        print(
            f"Iteration: {i}, Loss: {loss_val.item():0.2f}"
        )
    opt.step()
    opt.zero_grad()

Iteration: 0, Loss: 73.11
Iteration: 10, Loss: 48.06
Iteration: 20, Loss: 39.89
Iteration: 30, Loss: 37.01
Iteration: 40, Loss: 36.10
Iteration: 50, Loss: 35.78
Iteration: 60, Loss: 35.67
Iteration: 70, Loss: 35.64
Iteration: 80, Loss: 35.62
Iteration: 90, Loss: 35.62
Iteration: 100, Loss: 35.62

plot_fit(
    x_sample,
    y_sample,
    theta_learn_loc.detach(),
    r"Torch MAP",
)

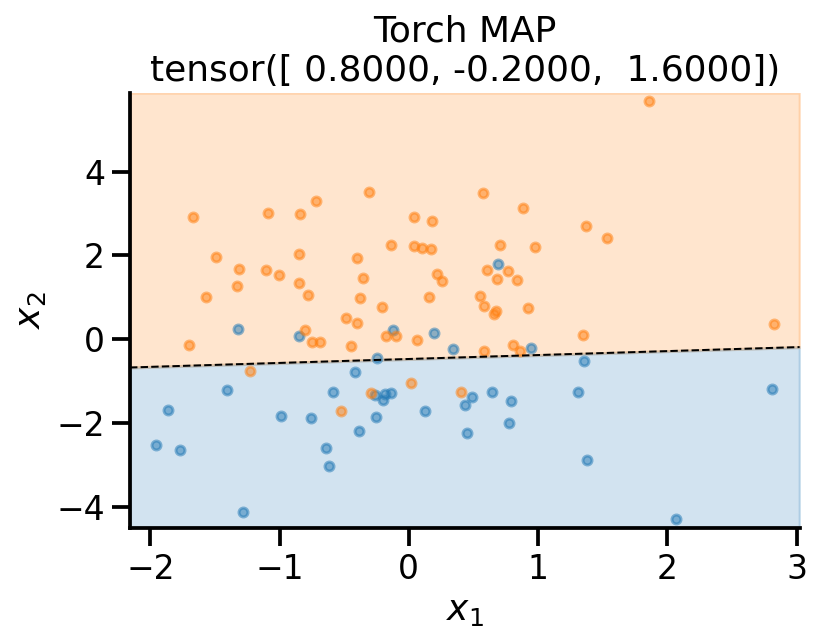
../../_images/2022-02-14-logistic-regression_23_0.png

References¶

Plotting code borrwed from here: https://scipython.com/blog/plotting-the-decision-boundary-of-a-logistic-regression-model/

previous

Probabilstic PCA using PyTorch distributions

next

Testing out some distributions in Tensorflow Probability